Viskosität
Unter der Viskosität versteht man die „Zähigkeit“ einer Flüssigkeit oder eines Gases. Sie resultiert aus den zwischenmolekularen Kräften in einem Fluid, ist also abhängig von der Kohäsion zwischen den Molekülen oder Teilchen. Man spricht daher auch von der inneren Reibung. Bei Feststoffen verwendet man stattdessen die Begriffe der Duktilität, Sprödigkeit und Plastizität.
Der Begriff Viskosität leitet sich von dem lateinischen Wort für Mistel "viscum" her, aus deren Beeren ein zäher Vogelleim hergestellt wurde.
Inhaltsverzeichnis |
Viskosität von Flüssigkeiten
Spricht man von Viskosität, soll in der Regel das Fließverhalten einer Flüssigkeit charakterisiert werden. Je höher die Viskosität dabei ist, desto dickflüssiger ist die Substanz. Diesen Effekt kann man sich vereinfacht durch die Bewegung zweier übereinander liegender, verzahnter Molekülschichten vorstellen (siehe Abb. Punkt 1). Beim Fließen gleiten die Moleküle aneinander vorbei, und um die Verzahnung zu überwinden benötigt man eine gewisse Kraft. Den Zusammenhang zwischen dieser Kraft und den Eigenschaften des vorliegenden Fluids definiert die Viskosität. Erkennbar wird dieser Zusammenhang besonders gut an der homologen Reihe der Alkane (kettenförmige Kohlenwasserstoffen), hier steigt die Viskosität mit der Kettenlänge und damit den zunehmenden intermolekular wirkenden van-der-Waals-Kräften kontinuierlich an. Bei den mittleren Alkanen (ab Nonan, neun C-Atome) hat sie bereits einen Wert ähnlich dem von Wasser.

Sehr gut veranschaulichen kann man sich die Viskosität auch an folgendem Beispiel: gleitet Wind über das Wasser eines Ozeans, erzeugt dies eine Bewegung der Wasserschicht an der Oberfläche. Je tiefer man nun taucht, desto ruhiger wird das Wasser, bis man einen Punkt erreicht, wo keine Strömung herrscht. Die einzelnen Flüssigkeitsschichten bewegen sich mit unterschiedlicher Geschwindigkeit (Korkenzieherströmung), es entsteht ein Geschwindigkeitsgradient (siehe Abb. Punkt 2):
Weht kein Wind mehr, bricht die Strömung zusammen, das Wasser ruht auch wieder an der Oberfläche. Dass die Flüssigkeit auch in tieferen Schichten trotz Wind an der Oberfläche praktisch ruht, ist Folge der inneren Reibung in der Flüssigkeit.
Die Viskosität der meisten Flüssigkeiten nimmt mit steigender Temperatur ab, oft ist sie proportional zu folgendem Term:
Wobei A eine flüssigkeitsspezifische Konstante und T die Temperatur ist.
Definition der Viskosität

Man stelle sich zwei im Abstand x angeordnete Platten der Fläche A vor. Zwischen diesen Platten befindet sich eine Flüssigkeit, die an beiden Platten haftet. In unserer Vorstellung soll der Raum mit der Flüssigkeit in Schichten unterteilt sein. Wird nun Platte 2 mit der Geschwindigkeit v bewegt, so bewegt sich die Schicht, in unmittelbarer Nachbarschaft zu Platte 2 auf Grund der Haftung ebenfallfs mit der Geschwindigkeit v. Da Platte 1 ruht, ruht auch ihre Nachbarschicht. Die innenliegenden Flüssigkeitsschichten gleiten mit unterschiedlichen Geschwindigkeiten aneinander vorbei. Die Geschwindigkeit nimmt von der ruhenden Platte zur bewegten zu. Im einfachsten Fall besteht eine lineare Abhängigkeit (siehe Abbildung). Von der obersten, an der Platte haftenden Schicht, geht eine Tangentialkraft auf die darunterliegende Schicht aus. Diese bewegt sich folglich mit der Geschwindigkeit v1. Diese Schicht wirkt wiederum auf die darunterliegende Schicht und bewegt sie mit der Geschwindigkeit v2.
Im Experiment lässt sich zeigen, dass die Kraft F, die nötig ist, um Platte 2 zu bewegen direkt proportional zu ihrer Fläche A, ihrer Geschwindigkeit v und antiproportional zu dem Abstand der Platten x ist:
-
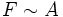 und
und
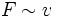 und
und

Hieraus ergibt sich
und als Gleichung
Die Proportionalitätskonstante η ist die dynamische Viskosität. Häufig wird sie auch nur als Viskosität bezeichnet. Ein Stoff hat also die Viskosität 1 Ns/m², wenn bei einer Größe der Platten von 1 m² und einem Plattenabstand von 1 m eine Kraft von 1 N benötigt wird, um die Platten mit einer Geschwindigkeit von 1 m/s gegeneinander zu verschieben.
Für die physikalische Einheit gilt:
![1{\rm N}=[\eta] \cdot\left(\frac{{\rm m}^2\,{\rm m}}{{\rm m}\,{\rm s}}\right) \Rightarrow [\eta] = \frac{{\rm N}\,{\rm s}}{{\rm m}^2}.](a52e7d4f20fe0b2dcff8ac2999946d4d.png)
Ist η unabhängig von der Geschwindigkeit v, so wird die Flüssigkeit als Newtonsche Flüssigkeit bezeichnet. Für diese Flüssigkeiten stellte sich das in Abbildung 2 gezeigte, lineare Geschwindigkeitsprofil ein. Ist η nicht von v unabhängig, so bezeichnet man die Flüssigkeit als nicht-Newtonsch.
Newtonsche Flüssigkeiten
Im folgenden wird der vereinfachte Zusammenhang gemäß dem
Newtonschen Viskositätsgesetz dargestellt, es wird dabei
stets
laminare Strömung sowie Temperatur- und Druckunabhängigkeit
der Flüssigkeitseigenschaften angenommen. Außerdem unterstellte
Newton eine
lineare Abhängigkeit des oben erläuterten
Geschwindigkeitsgradienten, der auch
Schergefälle
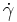 (manchmal auch mit D
bezeichnet) genannt wird:
(manchmal auch mit D
bezeichnet) genannt wird:

1: dilatantes Fluid
2: Newtonsche Fluid
3: Scherverdünnendes (pseudoplastisches) Fluid
4: Bingham-plastisches Fluid
5: Casson-plastisches Fluid
Verknüpft man dies mit der Schubspannung, erhält man folgenden Zusammenhang für die dynamische Viskosität:
Die Schubspannung τ ergibt sich aus der die Strömung bewirkenden Kraft bezogen auf die betroffene Angriffsfläche, die sich mit maximaler Geschwindigkeit bewegt. η wird bei Newtonschen Flüssigkeiten als Konstante angesehen. Viele Substanzen folgen diesem Gesetz jedoch nicht. Dabei unterscheidet man verschiedene Arten der Abweichung:
-
Strukturviskosität /
Dilatanz, dabei ist die Viskosität
η keine Konstante, sondern ändert sich mit dem
Schergefälle
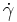
- Thixotropie / Rheopexie, hierbei zeigen sich zeitabhängige Strukturveränderungen, so dass je nach Zeitdauer seit der letzten Fließbewegung andere Viskositätswerte zu finden sind
- Fließgrenze, es muss erst eine gewisse Mindestschubspannung vorhanden sein, um ein Fließen zu erreichen (plastisches Fließen). Diese Art Fluid wird auch als Bingham-Fluid bezeichnet.
Derartige Fluide bezeichnet man als Nichtnewtonsche Fluide.
Im allgemeinen Fall muss das Schergefälle
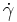 aus dem
Schwerwinkel in der Flüssigkeit berechnet werden und nicht
über den Geschwindigkeitsgradienten.
aus dem
Schwerwinkel in der Flüssigkeit berechnet werden und nicht
über den Geschwindigkeitsgradienten.
Darüber hinaus wird das Verhältnis zwischen der dynamischen Viskosität η und der Dichte ρ definiert als kinematische Viskosität:
SI-Einheit
Die SI-Einheit der
-
dynamischen Viskosität:
![[\eta] = \frac{\rm kg}{\rm m \cdot s} = {\rm Pa} \cdot {\rm s} = \frac{\rm Ns}{\rm m^2}](6e794c798838b1cf3b53bb18de423637.png)
- kinematischen Viskosität:
![[\nu] = \frac{\rm m^2}{\rm s}](02bf4fd293d056d8c0ebc96c381aa866.png)
Im
CGS-System wird für die dynamische Viskosität
Poise*
(P) verwendet, 10 P = 1 Pa s, für die kinematische Viskosität
das Stokes (St), 1 m2/s = 104 St.
*Das Poise (P) ist eine nichtgesetzliche Einheit der dynamischen Viskosität, benannt nach dem französischen Physiker und Mediziner Jean Louis Marie Poiseuille.
Typische Viskositätswerte
(η in [mPa s] bei 20 °C)
Petroleum 0,65 Pentan 0,232 Olivenöl ~ 102 Wasser 1,0 Hexan 0,320 Honig ~ 104 Quecksilber 1,5 Heptan 0,410 Sirup ~ 105 Traubensaft 2-5 Oktan 0,538 Polymerschmelzen ~ 103 bis 106 Blut (37 °C) 4-25 Nonan 0,710 Bitumen ~ 1011 Kaffeesahne ~10 Dekan 0,920 Glas (fest) ~ 1023 Paraffinöl 110–230 Ethanol 1,19 Glas (Verarbeitungstemp.) ~ 102 bis 104 Glycerin (rein) 1480 Asphalt 100000
Viskosität von Gasen
Auch für Gase lässt sich eine Viskosität definieren:
-
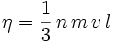 ,
mit der
freien Weglänge l
für die Gasteilchen, der Masse der Gasteilchen
m, der mittleren
Teilchengeschwindigkeit v
und der Teilchenzahldichte n.
,
mit der
freien Weglänge l
für die Gasteilchen, der Masse der Gasteilchen
m, der mittleren
Teilchengeschwindigkeit v
und der Teilchenzahldichte n.
Die Viskosität von Gasen ist unabhängig vom Druck. Dies gilt solange, wie die freie Weglänge klein gegenüber den Gefäßabmessungen und groß gegenüber den Molekülabmessungen ist. Mit anderen Worten: für ein sehr dünnes oder ein sehr dichtes Gas wird die Viskosität doch wieder vom Druck beziehungsweise der Dichte des Gases abhängig. Grundsätzlich abhängig ist die Viskosität aber von der Temperatur, da hier v mit der Temperatur zunimmt. Dieses Verhalten ist bei den meisten Flüssigkeiten genau entgegengesetzt. Für Luft liegen die Grenzen in der Größenordnung von einigen mm bis zu cm (zum Beispiel Lungenautomat beim Tauchen) und 0,4 nm (Moleküldurchmesser). Die folgende Tabelle listet zu einigen Gasen die Viskositäten und freien Weglängen auf.
| Gas | η (273 K) in µPa·s | l (1 atm) in nm |
| Luft | 17,1 | 59,8 |
| Sauerstoff (O2) | 19,2 | 63,3 |
| Kohlendioxid (CO2) | 13,8 | 39,0 |
| Stickstoff (N2) | 16,6 | 58,8 |
| Argon | 21,0 | 62,6 |
| Neon | 29,7 | 124,0 |
| Helium | 18,6 | 174,0 |
| Wasserstoff (H2) | 8,4 | 111,0 |
Die Abnahme der Viskosität mit der Temperatur nutzt man bei
Experimenten in
Windkanälen. Die Verkleinerung der Messmodelle reduziert die
Reynolds-Zahl*, die sich durch Kühlung kompensieren lässt.
*Die Reynolds-Zahl (Formelzeichen: Re) ist eine nach dem Physiker Osborne Reynolds benannte dimensionslose Kennzahl. Sie wird in der Strömungslehre verwendet und stellt das Verhältnis von Trägheits- zu Zähigkeitskräften dar. Für eine ideale Flüssigkeit ohne Viskosität ist das Verhältnis unendlich.
Kinetische Gastheorie
Nach Hirschfelder kann die Viskosität reiner Gase mit Hilfe der kinetischen Gastheorie* in einem großen Temperaturbereich (etwa von 200 bis 3000 Kelvin) berechnet werden.
Hierbei ist m die
Molekülmasse, kB
die
Boltzmann-Konstante**, T
die Temperatur, σ der
Lennard-Jones-Stoßdurchmesser und
 das reduzierte Stoßintegral, dass von reduzierten Temperatur
das reduzierte Stoßintegral, dass von reduzierten Temperatur
 abhängt. ε ist die Energie des
Lennard-Jones-Potenzials. Werte für die
Lennard-Jones-Parameter und das reduzierte Stoßintegral sind in
Lienhards Lehrbuch zur Wärmeübertragung in Kapitel 11
aufgeführt.
abhängt. ε ist die Energie des
Lennard-Jones-Potenzials. Werte für die
Lennard-Jones-Parameter und das reduzierte Stoßintegral sind in
Lienhards Lehrbuch zur Wärmeübertragung in Kapitel 11
aufgeführt.
*Die Kinetische Gastheorie ist ein Teilgebiet der
statistischen Mechanik. Sie erklärt die Gasgesetze und die
Eigenschaften von Gasen durch Bewegungsvorgänge ihrer Teilchen.
Die Kinetische Theorie offeriert eine Erklärung der
mikroskopischen Eigenschaften von Temperatur und Wärme,
wohingegen die Thermodynamik deren makroskopischen Eigenschaften
untersucht.
**Die Boltzmann-Konstante (Formelzeichen: kB oder k) ist die fundamentale Umrechnungskonstante zwischen Temperaturen und thermischen Energien. Sie ist benannt nach Ludwig Boltzmann und nicht zu verwechseln mit der Stefan-Boltzmann-Konstante.
Fluidität
Der Kehrwert der Viskosität ist die Fluidität
η − 1 mit der Einheit
![[\eta^{-1}]=\frac{\rm m \cdot s}{\rm kg}](75f4062d0c0c0373c8907edca3dd40f0.png) .
.

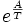
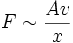
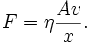

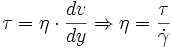
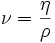


 ist:
ist: